Law of Conservation of Mass and Continuity Equation
by Dasa
. 25 Aug 2023
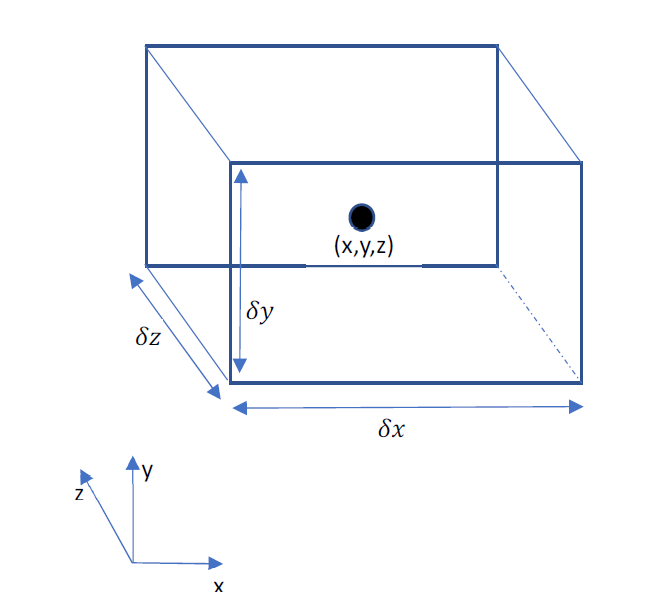
Consider a fluid volume with dimensions ∂ x \partial x ∂ x ∂ y \partial y ∂ y ∂ z \partial z ∂ z
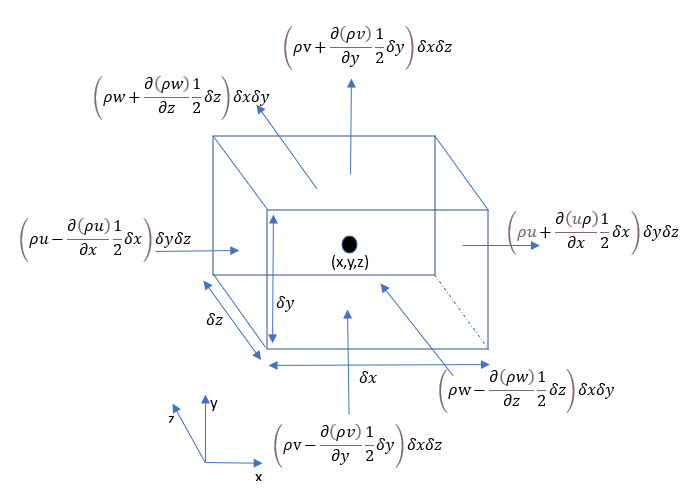
The mass flow rate(kg/s) across a face can be given as the product of density(kg/m3), velocity(m/s), and area (m2).
ρ ∗ u ∗ ∂ y ∂ z \begin{aligned}
\rho * u * \partial y \partial z
\end{aligned}
ρ ∗ u ∗ ∂ y ∂ z
The center is located at 1 2 ∂ x \frac{1}{2} \partial x 2 1 ∂ x 1 2 ∂ y \frac{1}{2} \partial y 2 1 ∂ y 1 2 ∂ z \frac{1}{2} \partial z 2 1 ∂ z
Taylor Series state that the change is f ( c ) f(c) f ( c ) x x x c c c
= f ( c ) + f ′ ( c ) . x \begin{aligned}
= f(c)+f^{\prime}(c).x
\end{aligned}
= f ( c ) + f ′ ( c ) . x
Similarly, we can write the change in ρu at a distance of 1 2 ∂ x \frac{1}{2} \partial x 2 1 ∂ x
1 2 ∂ x \frac{1}{2} \partial x 2 1 ∂ x
= f ( ρ u ) + f ′ ( ρ u ) . 1 2 ∂ x = f ( ρ u ) + ∂ ( ρ u ) ∂ x . 1 2 ∂ x \begin{aligned}
= f(\rho u) + f^{\prime}(\rho u) . \frac{1}{2} \partial x \\
= f(\rho u) + \frac{\partial (\rho u)}{\partial x} . \frac{1}{2} \partial x
\end{aligned}
= f ( ρ u ) + f ′ ( ρ u ) . 2 1 ∂ x = f ( ρ u ) + ∂ x ∂ ( ρ u ) . 2 1 ∂ x
1 2 ∂ x \frac{1}{2} \partial x 2 1 ∂ x
= f ( ρ u ) − f ′ ( ρ u ) . 1 2 ∂ x = f ( ρ u ) − ∂ ( ρ u ) ∂ x . 1 2 ∂ x \begin{aligned}
= f(\rho u) - f^{\prime}(\rho u) . \frac{1}{2} \partial x \\
= f(\rho u) - \frac{\partial (\rho u)}{\partial x} . \frac{1}{2} \partial x
\end{aligned}
= f ( ρ u ) − f ′ ( ρ u ) . 2 1 ∂ x = f ( ρ u ) − ∂ x ∂ ( ρ u ) . 2 1 ∂ x
The rate of increase in mass flow rate in a given time ∂ t \partial t ∂ t
=
The net change in mass flow rate
=
(The mass flow rate entering the element) – (The mass flow rate leaving the element)
=
∂ ρ ∂ t ∂ x ∂ y ∂ z \frac{\partial \rho}{\partial t} \partial x \partial y \partial z ∂ t ∂ ρ ∂ x ∂ y ∂ z
∂ ρ ∂ t ∂ x ∂ y ∂ z = \frac{\partial \rho}{\partial t} \partial x \partial y \partial z = ∂ t ∂ ρ ∂ x ∂ y ∂ z = ( ρ u − ∂ ( ρ u ) ∂ x . 1 2 ∂ x ) ∂ y ∂ z − ( ρ u + ∂ ( ρ u ) ∂ x . 1 2 ∂ x ) ∂ y ∂ z (\rho u - \frac{\partial (\rho u)}{\partial x} . \frac{1}{2} \partial x) \partial y \partial z - (\rho u + \frac{\partial (\rho u)}{\partial x} . \frac{1}{2} \partial x) \partial y \partial z ( ρ u − ∂ x ∂ ( ρ u ) . 2 1 ∂ x ) ∂ y ∂ z − ( ρ u + ∂ x ∂ ( ρ u ) . 2 1 ∂ x ) ∂ y ∂ z + ( ρ v − ∂ ( ρ v ) ∂ y . 1 2 ∂ y ) ∂ x ∂ z − ( ρ v + ∂ ( ρ v ) ∂ y . 1 2 ∂ y ) ∂ x ∂ z + (\rho v - \frac{\partial (\rho v)}{\partial y} . \frac{1}{2} \partial y) \partial x \partial z - (\rho v + \frac{\partial (\rho v)}{\partial y} . \frac{1}{2} \partial y) \partial x \partial z + ( ρ v − ∂ y ∂ ( ρ v ) . 2 1 ∂ y ) ∂ x ∂ z − ( ρ v + ∂ y ∂ ( ρ v ) . 2 1 ∂ y ) ∂ x ∂ z + ( ρ w − ∂ ( ρ w ) ∂ z . 1 2 ∂ z ) ∂ x ∂ y − ( ρ w + ∂ ( ρ w ) ∂ z . 1 2 ∂ z ) ∂ x ∂ y + (\rho w - \frac{\partial (\rho w)}{\partial z} . \frac{1}{2} \partial z) \partial x \partial y - (\rho w + \frac{\partial (\rho w)}{\partial z} . \frac{1}{2} \partial z) \partial x \partial y + ( ρ w − ∂ z ∂ ( ρ w ) . 2 1 ∂ z ) ∂ x ∂ y − ( ρ w + ∂ z ∂ ( ρ w ) . 2 1 ∂ z ) ∂ x ∂ y
= ( − ∂ ( ρ u ) ∂ x . 1 2 ∂ x ) ∂ y ∂ z − ( ∂ ( ρ u ) ∂ x . 1 2 ∂ x ) ∂ y ∂ z =(- \frac{\partial (\rho u)}{\partial x} . \frac{1}{2} \partial x) \partial y \partial z - (\frac{\partial (\rho u)}{\partial x} . \frac{1}{2} \partial x) \partial y \partial z = ( − ∂ x ∂ ( ρ u ) . 2 1 ∂ x ) ∂ y ∂ z − ( ∂ x ∂ ( ρ u ) . 2 1 ∂ x ) ∂ y ∂ z + ( − ∂ ( ρ v ) ∂ y . 1 2 ∂ y ) ∂ x ∂ z − ( ∂ ( ρ v ) ∂ y . 1 2 ∂ y ) ∂ x ∂ z + (- \frac{\partial (\rho v)}{\partial y} . \frac{1}{2} \partial y) \partial x \partial z - (\frac{\partial (\rho v)}{\partial y} . \frac{1}{2} \partial y) \partial x \partial z + ( − ∂ y ∂ ( ρ v ) . 2 1 ∂ y ) ∂ x ∂ z − ( ∂ y ∂ ( ρ v ) . 2 1 ∂ y ) ∂ x ∂ z + ( − ∂ ( ρ w ) ∂ z . 1 2 ∂ z ) ∂ x ∂ y − ( ∂ ( ρ w ) ∂ z . 1 2 ∂ z ) ∂ x ∂ y + (- \frac{\partial (\rho w)}{\partial z} . \frac{1}{2} \partial z) \partial x \partial y - (\frac{\partial (\rho w)}{\partial z} . \frac{1}{2} \partial z) \partial x \partial y + ( − ∂ z ∂ ( ρ w ) . 2 1 ∂ z ) ∂ x ∂ y − ( ∂ z ∂ ( ρ w ) . 2 1 ∂ z ) ∂ x ∂ y
= ( − ∂ ( ρ u ) ∂ x ∂ x ) ∂ y ∂ z =(- \frac{\partial (\rho u)}{\partial x} \partial x) \partial y \partial z = ( − ∂ x ∂ ( ρ u ) ∂ x ) ∂ y ∂ z + ( − ∂ ( ρ v ) ∂ y ∂ y ) ∂ x ∂ z + (- \frac{\partial (\rho v)}{\partial y} \partial y) \partial x \partial z + ( − ∂ y ∂ ( ρ v ) ∂ y ) ∂ x ∂ z + ( − ∂ ( ρ w ) ∂ z ∂ z ) ∂ x ∂ y + (- \frac{\partial (\rho w)}{\partial z} \partial z) \partial x \partial y + ( − ∂ z ∂ ( ρ w ) ∂ z ) ∂ x ∂ y
We can write the above equation as below
∂ ρ ∂ t ∂ x ∂ y ∂ z = − ∂ ( ρ u ) ∂ x ∂ x ∂ y ∂ z − ∂ ( ρ v ) ∂ y ∂ x ∂ y ∂ z − ∂ ( ρ w ) ∂ z ∂ x ∂ y ∂ z \frac{\partial \rho}{\partial t} \partial x \partial y \partial z = - \frac{\partial (\rho u)}{\partial x} \partial x \partial y \partial z - \frac{\partial (\rho v)}{\partial y} \partial x \partial y \partial z - \frac{\partial (\rho w)}{\partial z} \partial x \partial y \partial z ∂ t ∂ ρ ∂ x ∂ y ∂ z = − ∂ x ∂ ( ρ u ) ∂ x ∂ y ∂ z − ∂ y ∂ ( ρ v ) ∂ x ∂ y ∂ z − ∂ z ∂ ( ρ w ) ∂ x ∂ y ∂ z
∂ ρ ∂ t = − ∂ ( ρ u ) ∂ x − ∂ ( ρ v ) ∂ y − ∂ ( ρ w ) ∂ z \frac{\partial \rho}{\partial t} = - \frac{\partial (\rho u)}{\partial x} - \frac{\partial (\rho v)}{\partial y} - \frac{\partial (\rho w)}{\partial z} ∂ t ∂ ρ = − ∂ x ∂ ( ρ u ) − ∂ y ∂ ( ρ v ) − ∂ z ∂ ( ρ w )
∂ ρ ∂ t + ∂ ( ρ u ) ∂ x + ∂ ( ρ v ) ∂ y + ∂ ( ρ w ) ∂ z = 0 \frac{\partial \rho}{\partial t} + \frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z} = 0 ∂ t ∂ ρ + ∂ x ∂ ( ρ u ) + ∂ y ∂ ( ρ v ) + ∂ z ∂ ( ρ w ) = 0
Using the divergence rule
∂ ρ ∂ t + d i v ( ρ U ) = 0 \frac{\partial \rho}{\partial t} + div(\rho U) = 0 ∂ t ∂ ρ + d i v ( ρ U ) = 0
The above equation is an unsteady, three-dimensional mass conservation or continuity equation at a point in a compressible fluid.
The first term is “the rate of change in density with respect to time.”
The second term is “the net flow of mass out of the element across its boundaries,” known as the “convective term.”
For incompressible fluid the change in density is zero or it is constant.
d i v ( U ) = 0 div(U) = 0 d i v ( U ) = 0