Momentum equation in a 3D particle and its surface & body forces

Newton’s second law states that “the changes in momentum in a fluid particle is equal to the sum of all the forces acting on it.”

$\begin{Bmatrix} \text{The Rate Of Increase } \\ \text{ of momentum of }\\ \text{fluid particle} \end{Bmatrix} = \begin{Bmatrix} \text{Sum of forces } \\ \text{ acting on the }\\ \text{fluid particle} \end{Bmatrix}$

Changes in momentum in the x, y, and z directions are given below.

$\rho \frac{Du}{Dt}$, $\rho \frac{Dv}{Dt}$, $\rho \frac{Dw}{Dt}$

Refer Law of Conservation of Momentum and Energy for details.

The forces acting on a fluid particle are

Surface forces

Pressure forces - normal stress on the surfaces Viscous forces - normal and parallel to the surfaces.

Body forces

Gravity forces Centrifugal forces Coriolis forces Electromagnetic forces

In the momentum equation, surface forces were added as a separate term, and body forces were treated as source terms.

The below image shows the Viscous forces acting on the 3D fluid element surfaces.

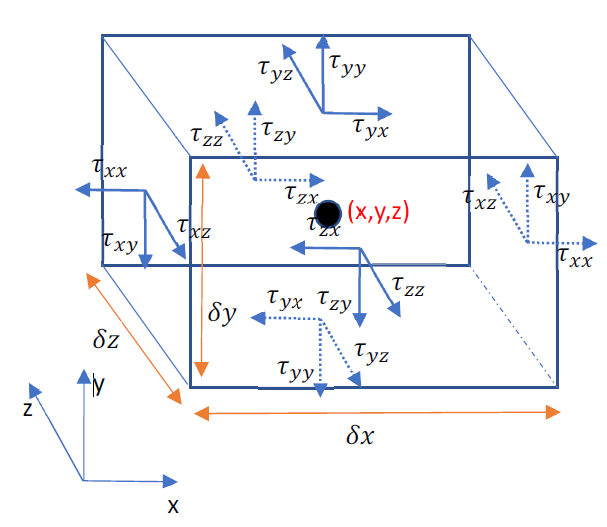
$\tau_{xx}$, $\tau_{yy}$, and $\tau_{zz}$ are normal stresses; all other terms are shear stresses. For example,

$\tau_{xy}$ denotes the Viscous force acting in the direction of y on a plane normal to x.

The image below shows the Pressure and Viscous forces acting in the x-direction.

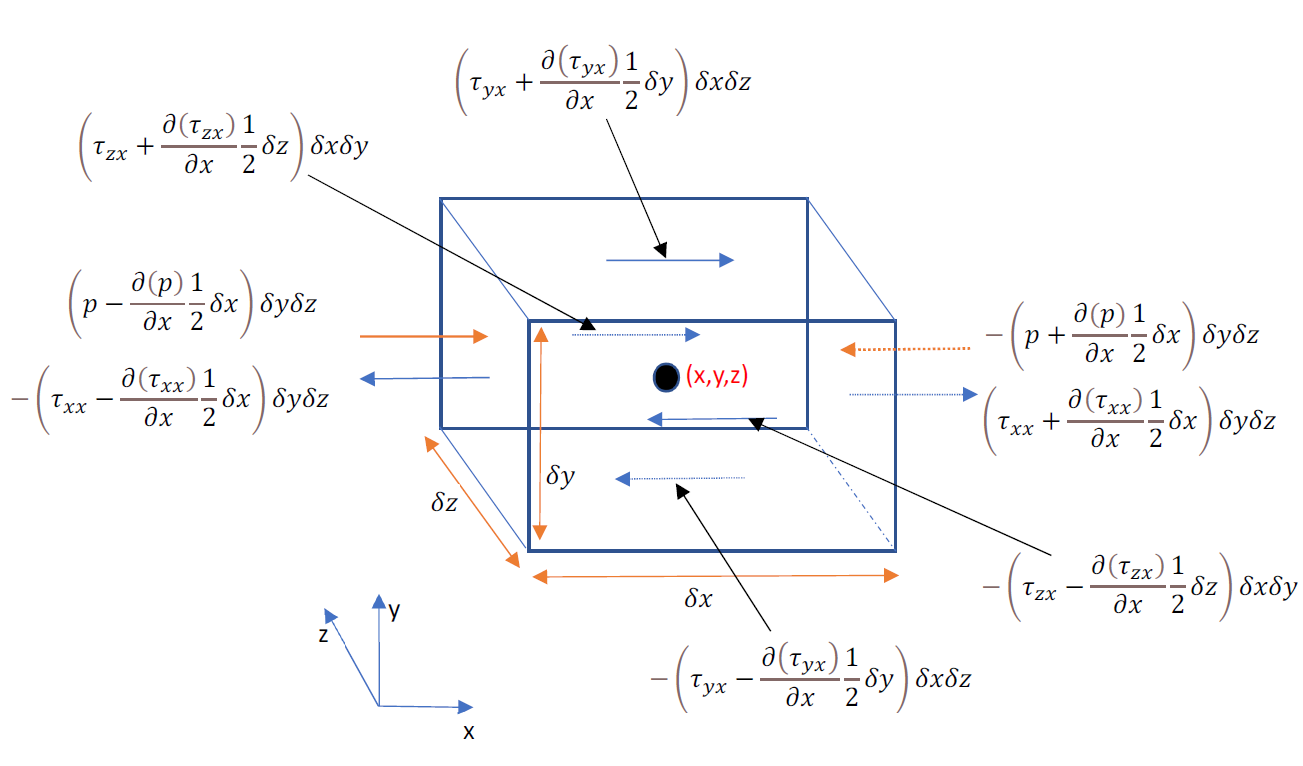
The negative sign indicates the opposite of the direction of co-ordinates. The stresses are force per unit area, and the unit can be N/m². In the above equation, “p” is a compressive stress, and “$\tau_{xx}$” is a tensile stress.

The equation for x-momentum with surface forces can be expressed in the following manner.

$\begin{array}{c} \rho \frac{Du}{Dt} &= (p - \frac{\partial (p)}{\partial x} \frac{1}{2} \partial x) \partial y \partial z - (p + \frac{\partial (p)}{\partial x} \frac{1}{2} \partial x) \partial y \partial z\\\\ &-(\tau_{xx} - \frac{\partial (\tau_{xx})}{\partial x} \frac{1}{2} \partial x) \partial y \partial z + (\tau_{xx} + \frac{\partial (\tau_{xx})}{\partial x} \frac{1}{2} \partial x) \partial y \partial z\\\\ &-(\tau_{yx} - \frac{\partial (\tau_{yx})}{\partial y} \frac{1}{2} \partial y) \partial x \partial z + (\tau_{yx} + \frac{\partial (\tau_{yx})}{\partial y} \frac{1}{2} \partial y) \partial x \partial z\\\\ &-(\tau_{zx} - \frac{\partial (\tau_{zx})}{\partial z} \frac{1}{2} \partial z) \partial x \partial y + (\tau_{zx} + \frac{\partial (\tau_{zx})}{\partial z} \frac{1}{2} \partial z) \partial x \partial y\\\\ \\\\ &=-[(\frac{\partial (p)}{\partial x} \partial x) \partial y \partial z] + (\frac{\partial (\tau_{xx})}{\partial x} \partial x) \partial y \partial z \\\\ &+ (\frac{\partial (\tau_{yx})}{\partial y} \partial y) \partial x \partial z + (\frac{\partial (\tau_{zx})}{\partial z} \partial z) \partial x \partial y \end{array}$

Divide all the terms by $\partial x \partial y \partial z$ (unit volume) gives the momentum forces per unit volume.

$\begin{array}{c} \rho \frac{Du}{Dt} &= -(\frac{\partial (p)}{\partial x}) + (\frac{\partial (\tau_{xx})}{\partial x}) + (\frac{\partial (\tau_{yx})}{\partial y}) + (\frac{\partial (\tau_{zx})}{\partial z})\\\\ &= \frac{\partial (-p + \tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} \end{array}$

When we the body forces ($S_{Mx}$) to the above equation we get

$\begin{array}{c} \rho \frac{Du}{Dt} = \frac{\partial (-p + \tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} + S_{Mx} \end{array}$

Similarly the y-momentum and z-momentum can be written as below.

$\begin{array}{c} \rho \frac{Dv}{Dt} = \frac{\partial (\tau_{xx})}{\partial x} + \frac{\partial (-p + \tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} + S_{My}\\\\ \rho \frac{Dw}{Dt} = \frac{\partial (\tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (-p+\tau_{zx})}{\partial z} + S_{Mz}\\\\ \end{array}$