When we compute the divergence of a velocity vector in a finite volume, it gives a scalar value that is the mass flux. Here the scalar value is mass flux per unit of time.

Consider a velocity vector of

$U = u\space i + v\space j + w\space k$

The Nabla is equal to

$\nabla = (\dfrac{\partial}{\partial x} i + \dfrac{\partial}{\partial y} j + \dfrac{\partial}{\partial z} k)$

Then the divergent of U is

$\nabla . U = div\space U = (\dfrac{\partial}{\partial x} i + \dfrac{\partial}{\partial y} j + \dfrac{\partial}{\partial z} k) . U$
$\qquad = (\dfrac{\partial}{\partial x} i + \dfrac{\partial}{\partial y} j + \dfrac{\partial}{\partial z} k) . (u\space i + v\space j + w\space k)$
$\qquad = (\dfrac{\partial}{\partial x} u + \dfrac{\partial}{\partial y} v + \dfrac{\partial}{\partial z} w)$

If we dot a Nabla with a vector we get a vector that is called divergence.

Divergence theorem:

It states that the accumulation of a vector in a finite volume is equal to the sum of that vector over the surfaces.
Consider an infinitesimal volume having sides as dx, dy, and dz as below.

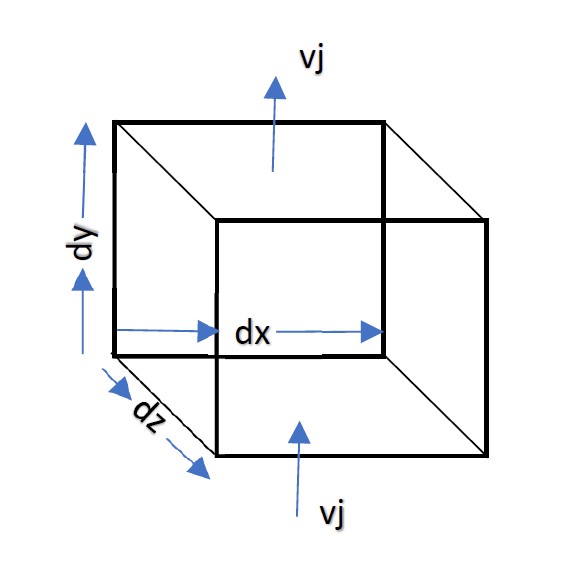
And a velocity vector vj enters the surface dS (=dxdz) and leaves at the opposite surface located at a distance of dy. Then change is the finite volume is the integral over the surfaces

$= vi\space dx\space dz - (vi+\dfrac{\partial}{\partial y} \space vj\space j\space dy) \space dx \space dz$

$= -\dfrac{\partial}{\partial y} \space vj \space j \space dy \space dx \space dz$

$= \dfrac{\partial}{\partial y} \space v \space dV$

When we sum the other two faces, we get

$= (\dfrac{\partial}{\partial x} \space u + \dfrac{\partial}{\partial y} \space v + \dfrac{\partial}{\partial z} \space w) \space dV$

$= \nabla \space . \space U dV$

Note: Here, we have yet to prove that the quantity calculated is independent of the coordinate system.
When a vector field has zero divergences, it is said to be “Solenoidal”.

The divergence theorem states that for any closed surfaces, the net total flux through the surfaces must be zero.

Please read this page for Gradient and Laplacian.