Gradient of a Scalar

The gradient is the change in quantity with respect to distance.

For example, heat is reduced when we move away from a heat source.

In other words, Gradient is the partial derivative of all the components of a function. If $\phi$ is the property of fluid then $grad(\phi)$ can be written as

$grad(\phi) = \frac{\partial \phi}{\partial x} + \frac{\partial \phi}{\partial y} + \frac{\partial \phi}{\partial z}$

In other words, if ‘f’ is a function of (x, y, z), then the Gradient of ‘f’ is a package of all the partial derivatives.

The Gradient will always increase the Tensor value by one. That means a Gradient of a scalar will give a vector (Tensor of value 1), and the Gradient of the vector will give a Tensor of value 2.

The gradient will determine the direction of a function with the greatest change. Through this direction, we can reach the peak of that function in the shortest distance from any point (the direction of the steepest ascent). The length of the gradient vector tells the steepness of the vector.

Consider a function f (x, y, z) in 3D. Assume it is a paraboloid equation that follows x² + y² - z when we plot z for various x & y values.

z = x² + y²

And the plot looks as below.

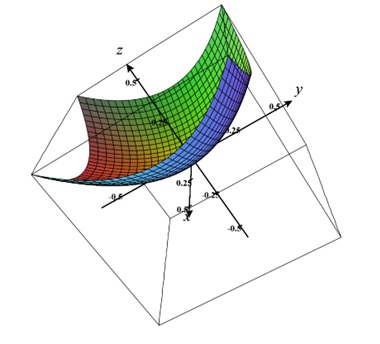
Then the gradient of z is the sum of all the partial derivatives, which denotes the directional vector through which we can reach the highest peak with the shortest distance.

$\nabla z = (\dfrac{\partial}{\partial x} i + \dfrac{\partial}{\partial y} j)(x^2 + y^2) = (2x\space i+ 2y \space j)$

For any x and y values, (2x i+2y j) is the direction through which we can reach the highest peak with the shortest distance.

The vector’s length is the vector’s modulus, denoting the steepness.

$\vert\nabla z\vert = \sqrt{(2x)^2 + (2y)^2}$

• Positive Gradient: is the direction through which the height increases fast in other words it is the direction of the steepest ascent.

• Negative Gradient: is the exact opposite of positive Gradient and it is the direction of the steepest descent.

• Zero Gradient: When the function is constant, we get zero Gradient. If we move the function in any direction and we get constant value when the Gradient zero.

Mathematically we say that the partial derivative of all the components is zero if the Gradient is zero.
For a constant velocity U, the grad U is normal to the surface everywhere.

Please read this page for Divergence and Laplacian.