Momentum equation in a 3D particle and its surface & body forces
by Dasa
. 01 Sep 2023
Newton’s second law states that “the changes in momentum in a fluid particle is equal to
{ T h e R a t e O f I n c r e a s e o f m o m e n t u m o f f l u i d p a r t i c l e } = { S u m o f f o r c e s a c t i n g o n t h e f l u i d p a r t i c l e } \begin{Bmatrix}
\text{The Rate Of Increase } \\
\text{ of momentum of }\\
\text{fluid particle}
\end{Bmatrix}
=
\begin{Bmatrix}
\text{Sum of forces } \\
\text{ acting on the }\\
\text{fluid particle}
\end{Bmatrix}
⎩ ⎨ ⎧ T h e R a t e O f I n c r e a s e o f m o m e n t u m o f f l u i d p a r t i c l e ⎭ ⎬ ⎫ = ⎩ ⎨ ⎧ S u m o f f o r c e s a c t i n g o n t h e f l u i d p a r t i c l e ⎭ ⎬ ⎫
Changes in momentum in the x, y, and z directions are given below.
ρ D u D t \rho \frac{Du}{Dt} ρ D t D u ρ D v D t \rho \frac{Dv}{Dt} ρ D t D v ρ D w D t \rho \frac{Dw}{Dt} ρ D t D w
Refer Law of Conservation of Momentum and Energy for details.
The forces acting on a fluid particle are
Surface forces
Pressure forces - normal stress on the surfaces
Body forces
Gravity forces
In the momentum equation, surface forces were added as a separate term , and body forcessource terms.
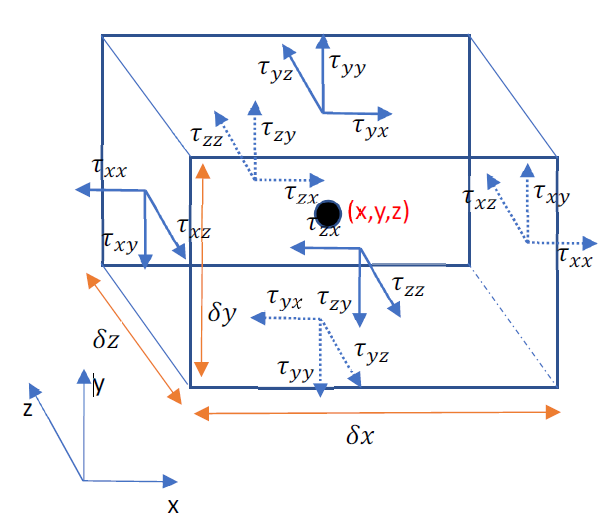
The below image shows the Viscous forces acting on the 3D fluid element surfaces.
τ x x \tau_{xx} τ x x τ y y \tau_{yy} τ y y τ z z \tau_{zz} τ z z normal stresses; all other terms are shear stresses. For example,
τ x y \tau_{xy} τ x y
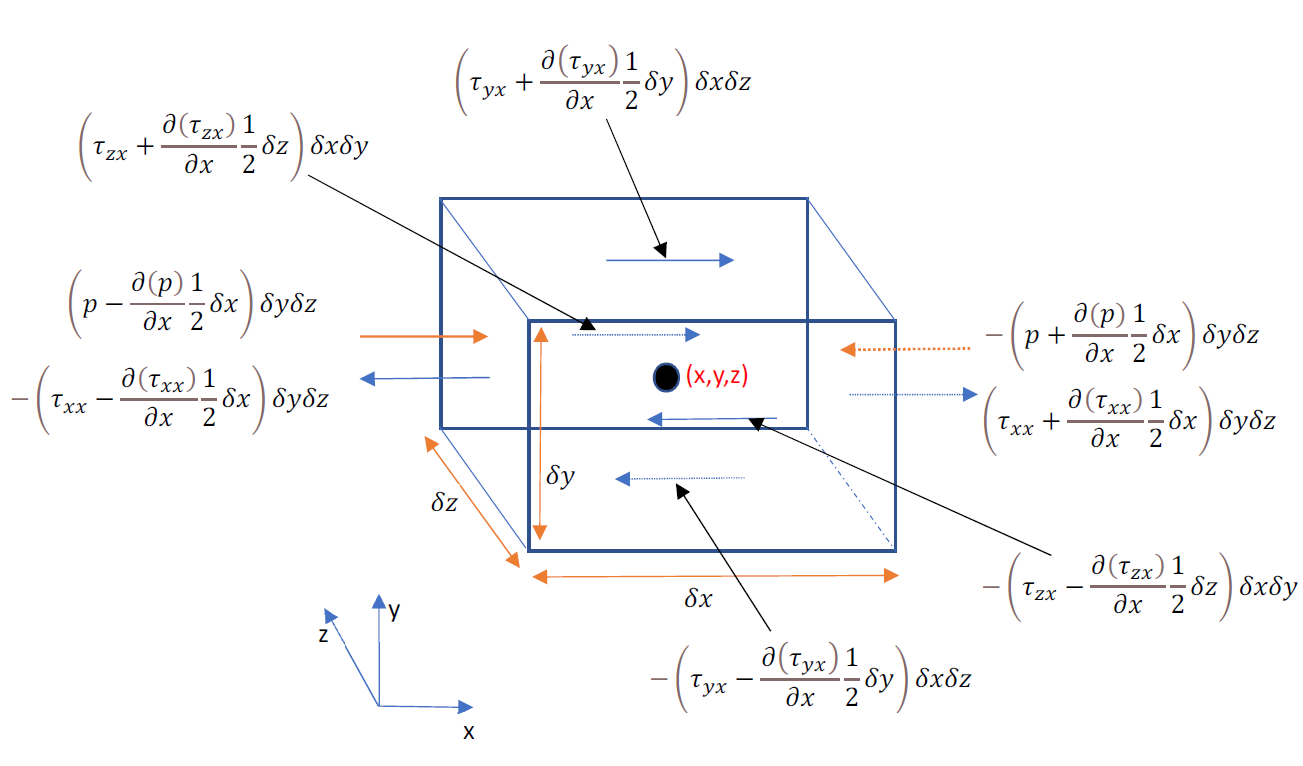
The image below shows the Pressure and Viscous forces acting in the x-direction.
The negative sign indicates the opposite of the direction of co-ordinates. The stresses are force per unit area, and the unit can be N/m². In the above equation, “p” is a compressive stress, and “τ x x \tau_{xx} τ x x
The equation for x-momentum with surface forces can be expressed in the following manner.
ρ D u D t = ( p − ∂ ( p ) ∂ x 1 2 ∂ x ) ∂ y ∂ z − ( p + ∂ ( p ) ∂ x 1 2 ∂ x ) ∂ y ∂ z − ( τ x x − ∂ ( τ x x ) ∂ x 1 2 ∂ x ) ∂ y ∂ z + ( τ x x + ∂ ( τ x x ) ∂ x 1 2 ∂ x ) ∂ y ∂ z − ( τ y x − ∂ ( τ y x ) ∂ y 1 2 ∂ y ) ∂ x ∂ z + ( τ y x + ∂ ( τ y x ) ∂ y 1 2 ∂ y ) ∂ x ∂ z − ( τ z x − ∂ ( τ z x ) ∂ z 1 2 ∂ z ) ∂ x ∂ y + ( τ z x + ∂ ( τ z x ) ∂ z 1 2 ∂ z ) ∂ x ∂ y = − [ ( ∂ ( p ) ∂ x ∂ x ) ∂ y ∂ z ] + ( ∂ ( τ x x ) ∂ x ∂ x ) ∂ y ∂ z + ( ∂ ( τ y x ) ∂ y ∂ y ) ∂ x ∂ z + ( ∂ ( τ z x ) ∂ z ∂ z ) ∂ x ∂ y \begin{array}{c}
\rho \frac{Du}{Dt} &= (p - \frac{\partial (p)}{\partial x} \frac{1}{2} \partial x) \partial y \partial z - (p + \frac{\partial (p)}{\partial x} \frac{1}{2} \partial x) \partial y \partial z\\\\
&-(\tau_{xx} - \frac{\partial (\tau_{xx})}{\partial x} \frac{1}{2} \partial x) \partial y \partial z + (\tau_{xx} + \frac{\partial (\tau_{xx})}{\partial x} \frac{1}{2} \partial x) \partial y \partial z\\\\
&-(\tau_{yx} - \frac{\partial (\tau_{yx})}{\partial y} \frac{1}{2} \partial y) \partial x \partial z + (\tau_{yx} + \frac{\partial (\tau_{yx})}{\partial y} \frac{1}{2} \partial y) \partial x \partial z\\\\
&-(\tau_{zx} - \frac{\partial (\tau_{zx})}{\partial z} \frac{1}{2} \partial z) \partial x \partial y + (\tau_{zx} + \frac{\partial (\tau_{zx})}{\partial z} \frac{1}{2} \partial z) \partial x \partial y\\\\
\\\\
&=-[(\frac{\partial (p)}{\partial x} \partial x) \partial y \partial z] + (\frac{\partial (\tau_{xx})}{\partial x} \partial x) \partial y \partial z \\\\
&+ (\frac{\partial (\tau_{yx})}{\partial y} \partial y) \partial x \partial z + (\frac{\partial (\tau_{zx})}{\partial z} \partial z) \partial x \partial y
\end{array} ρ D t D u = ( p − ∂ x ∂ ( p ) 2 1 ∂ x ) ∂ y ∂ z − ( p + ∂ x ∂ ( p ) 2 1 ∂ x ) ∂ y ∂ z − ( τ x x − ∂ x ∂ ( τ x x ) 2 1 ∂ x ) ∂ y ∂ z + ( τ x x + ∂ x ∂ ( τ x x ) 2 1 ∂ x ) ∂ y ∂ z − ( τ y x − ∂ y ∂ ( τ y x ) 2 1 ∂ y ) ∂ x ∂ z + ( τ y x + ∂ y ∂ ( τ y x ) 2 1 ∂ y ) ∂ x ∂ z − ( τ z x − ∂ z ∂ ( τ z x ) 2 1 ∂ z ) ∂ x ∂ y + ( τ z x + ∂ z ∂ ( τ z x ) 2 1 ∂ z ) ∂ x ∂ y = − [ ( ∂ x ∂ ( p ) ∂ x ) ∂ y ∂ z ] + ( ∂ x ∂ ( τ x x ) ∂ x ) ∂ y ∂ z + ( ∂ y ∂ ( τ y x ) ∂ y ) ∂ x ∂ z + ( ∂ z ∂ ( τ z x ) ∂ z ) ∂ x ∂ y
Divide all the terms by ∂ x ∂ y ∂ z \partial x \partial y \partial z ∂ x ∂ y ∂ z
ρ D u D t = − ( ∂ ( p ) ∂ x ) + ( ∂ ( τ x x ) ∂ x ) + ( ∂ ( τ y x ) ∂ y ) + ( ∂ ( τ z x ) ∂ z ) = ∂ ( − p + τ x x ) ∂ x + ∂ ( τ y x ) ∂ y + ∂ ( τ z x ) ∂ z \begin{array}{c}
\rho \frac{Du}{Dt} &= -(\frac{\partial (p)}{\partial x}) + (\frac{\partial (\tau_{xx})}{\partial x}) + (\frac{\partial (\tau_{yx})}{\partial y}) + (\frac{\partial (\tau_{zx})}{\partial z})\\\\
&= \frac{\partial (-p + \tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z}
\end{array} ρ D t D u = − ( ∂ x ∂ ( p ) ) + ( ∂ x ∂ ( τ x x ) ) + ( ∂ y ∂ ( τ y x ) ) + ( ∂ z ∂ ( τ z x ) ) = ∂ x ∂ ( − p + τ x x ) + ∂ y ∂ ( τ y x ) + ∂ z ∂ ( τ z x )
When we the body forces (S M x S_{Mx} S M x to the above equation we get
ρ D u D t = ∂ ( − p + τ x x ) ∂ x + ∂ ( τ y x ) ∂ y + ∂ ( τ z x ) ∂ z + S M x \begin{array}{c}
\rho \frac{Du}{Dt} = \frac{\partial (-p + \tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} + S_{Mx}
\end{array} ρ D t D u = ∂ x ∂ ( − p + τ x x ) + ∂ y ∂ ( τ y x ) + ∂ z ∂ ( τ z x ) + S M x
Similarly the y-momentum and z-momentum can be written as below.
ρ D v D t = ∂ ( τ x x ) ∂ x + ∂ ( − p + τ y x ) ∂ y + ∂ ( τ z x ) ∂ z + S M y ρ D w D t = ∂ ( τ x x ) ∂ x + ∂ ( τ y x ) ∂ y + ∂ ( − p + τ z x ) ∂ z + S M z \begin{array}{c}
\rho \frac{Dv}{Dt} = \frac{\partial (\tau_{xx})}{\partial x} + \frac{\partial (-p + \tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} + S_{My}\\\\
\rho \frac{Dw}{Dt} = \frac{\partial (\tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (-p+\tau_{zx})}{\partial z} + S_{Mz}\\\\
\end{array} ρ D t D v = ∂ x ∂ ( τ x x ) + ∂ y ∂ ( − p + τ y x ) + ∂ z ∂ ( τ z x ) + S M y ρ D t D w = ∂ x ∂ ( τ x x ) + ∂ y ∂ ( τ y x ) + ∂ z ∂ ( − p + τ z x ) + S M z