Energy equation in Three Dimension
by Dasa
. 01 Sep 2023
The first law of thermodynamics states that the change in internal energy equals the work done, and change is heat transfer.
Change in total (Specific) energy (E) of a fluid particle = Work done by the fluid particle + change in heat of fluid particle.
{ C h a n g e i n S p e c i f i c e n e r g y ( E ) o f a f l u i d p a r t i c l e } = { W o r k d o n e b y t h e f l u i d p a r t i c l e } + { c h a n g e i n h e a t o f t h e f l u i d p a r t i c l e } \begin{aligned}
\begin{Bmatrix}
\text{Change in Specific } \\
\text{energy (E) of a}\\
\text{fluid particle}
\end{Bmatrix}
=
\begin{Bmatrix}
\text{Work done } \\
\text{by the } \\
\text{fluid particle}
\end{Bmatrix}
+
\begin{Bmatrix}
\text{change in heat } \\
\text{of the } \\
\text{fluid particle}
\end{Bmatrix}
\end{aligned}
⎩ ⎨ ⎧ C h a n g e i n S p e c i f i c e n e r g y ( E ) o f a f l u i d p a r t i c l e ⎭ ⎬ ⎫ = ⎩ ⎨ ⎧ W o r k d o n e b y t h e f l u i d p a r t i c l e ⎭ ⎬ ⎫ + ⎩ ⎨ ⎧ c h a n g e i n h e a t o f t h e f l u i d p a r t i c l e ⎭ ⎬ ⎫
Change in Specific energy (E) of a fluid particle is
ρ D E D t \rho \frac{D E} {D t} ρ D t D E
The specific energy (E) is equal to the sum of internl energy (i), kinetic energy (1 2 ( u 2 + v 2 + w 2 ) \frac{1}{2}(u^2+v^2+w^2) 2 1 ( u 2 + v 2 + w 2 )
If the potential energy due to gravitational force is considered as source term we can define the Specific energy as below
E = i + 1 2 ( u 2 + v 2 + w 2 ) E = i + \frac{1}{2}(u^2+v^2+w^2) E = i + 2 1 ( u 2 + v 2 + w 2 )
Work done
Work done by the fluid particle is equal to the product of the velocity and the forces.
We get the below equation when we take x-momentum with out the source term from Momentum equation in a 3D particle and its surface & body forces and multiply it by velcity u.
∂ [ u ( − p + τ x x ) ] ∂ x + ∂ ( u τ y x ) ∂ y + ∂ ( u τ z x ) ∂ z \begin{array}{c}
\frac{\partial [u(-p + \tau_{xx})]}{\partial x} + \frac{\partial (u \tau_{yx})}{\partial y} + \frac{\partial (u \tau_{zx})}{\partial z}
\end{array} ∂ x ∂ [ u ( − p + τ x x ) ] + ∂ y ∂ ( u τ y x ) + ∂ z ∂ ( u τ z x )
Similary we can do for y and z directions as below
∂ ( v τ x x ) ∂ x + ∂ [ v ( − p + τ y x ) ] ∂ y + ∂ ( v τ z x ) ∂ z ∂ ( w τ x x ) ∂ x + ∂ ( w τ y x ) ∂ y + ∂ [ w ( − p + τ z x ) ] ∂ z \begin{array}{c}
\frac{\partial (v \tau_{xx})}{\partial x} + \frac{\partial [v(-p + \tau_{yx})]}{\partial y} + \frac{\partial (v \tau_{zx})}{\partial z} \\\\
\frac{\partial (w\tau_{xx})}{\partial x} + \frac{\partial (w\tau_{yx})}{\partial y} + \frac{\partial [w(-p+\tau_{zx})]}{\partial z}
\end{array} ∂ x ∂ ( v τ x x ) + ∂ y ∂ [ v ( − p + τ y x ) ] + ∂ z ∂ ( v τ z x ) ∂ x ∂ ( w τ x x ) + ∂ y ∂ ( w τ y x ) + ∂ z ∂ [ w ( − p + τ z x ) ]
Since,
− ∂ ( u p ) ∂ x − ∂ ( v p ) ∂ y − ∂ ( w p ) ∂ z = − d i v ( p U ) \begin{array}{c}
-\frac{\partial (up)}{\partial x} -\frac{\partial (vp)}{\partial y} -\frac{\partial (wp)}{\partial z} = - div(pU)
\end{array} − ∂ x ∂ ( u p ) − ∂ y ∂ ( v p ) − ∂ z ∂ ( w p ) = − d i v ( p U )
We can write the total work done by the fluid particle due to surface forces as below
− d i v ( p U ) + ∂ ( u τ x x ) ∂ x + ∂ ( u τ y x ) ∂ y + ∂ ( u τ z x ) ∂ z + ∂ ( v τ x x ) ∂ x + ∂ ( v τ y x ) ∂ y + ∂ ( v τ z x ) ∂ z + ∂ ( w τ x x ) ∂ x + ∂ ( w τ y x ) ∂ y + ∂ ( w τ z x ) ∂ z = > E q − ( 1 ) \begin{aligned}
-div(pU) + \frac{\partial (u\tau_{xx})}{\partial x} + \frac{\partial (u \tau_{yx})}{\partial y} + \frac{\partial (u \tau_{zx})}{\partial z} \\
+ \frac{\partial (v \tau_{xx})}{\partial x} + \frac{\partial (v \tau_{yx})}{\partial y} + \frac{\partial (v \tau_{zx})}{\partial z} \\
+ \frac{\partial (w\tau_{xx})}{\partial x} + \frac{\partial (w\tau_{yx})}{\partial y} + \frac{\partial (w \tau_{zx})}{\partial z}\\
=>Eq-(1)
\end{aligned} − d i v ( p U ) + ∂ x ∂ ( u τ x x ) + ∂ y ∂ ( u τ y x ) + ∂ z ∂ ( u τ z x ) + ∂ x ∂ ( v τ x x ) + ∂ y ∂ ( v τ y x ) + ∂ z ∂ ( v τ z x ) + ∂ x ∂ ( w τ x x ) + ∂ y ∂ ( w τ y x ) + ∂ z ∂ ( w τ z x ) = > E q − ( 1 )
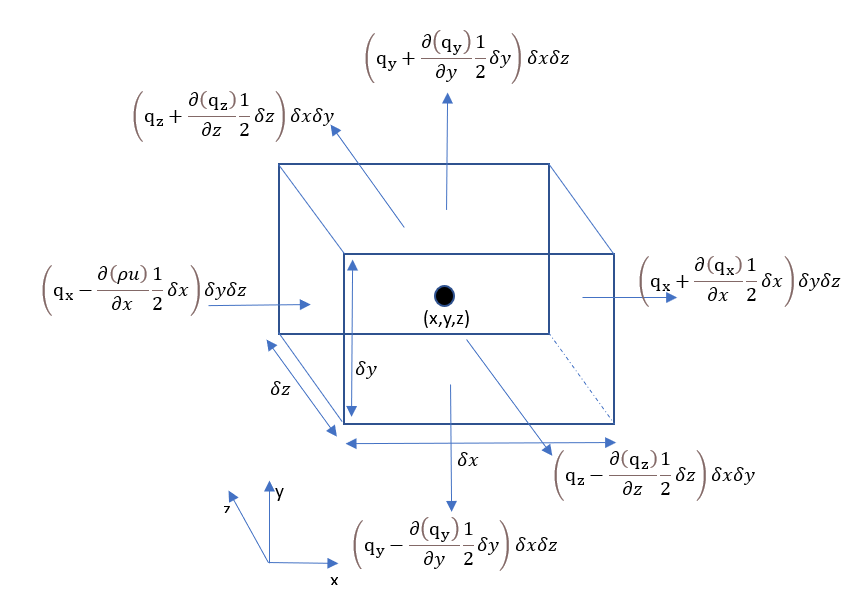
Energy flux due to heat conduction
Similar to the conservation of mass we can define the energy flux due to heat conduction as below
Now the total heatflux per unit volume can be expressed with below equation
− ∂ q x ∂ x − ∂ q y ∂ y − ∂ q z ∂ z = − d i v ( q ) \begin{array}{c}
-\frac{\partial q_{x}}{\partial x} - \frac{\partial q_{y}}{\partial y} - \frac{\partial q_{z}}{\partial z} = -div(q)
\end{array} − ∂ x ∂ q x − ∂ y ∂ q y − ∂ z ∂ q z = − d i v ( q )
Fourier law gives the flux due to heat condution (Refer Heat Transfer ) as below.
q x = − k ∂ T ∂ x q_{x} = -k \frac{\partial T}{\partial x} q x = − k ∂ x ∂ T q y = − k ∂ T ∂ y q_{y} = -k \frac{\partial T}{\partial y} q y = − k ∂ y ∂ T q z = − k ∂ T ∂ z q_{z} = -k \frac{\partial T}{\partial z} q z = − k ∂ z ∂ T
The same can be written in vector form as below
q = − k g r a d ( T ) q = -k \space grad(T) q = − k g r a d ( T )
So, we can say
− d i v ( q ) = d i v ( k g r a d ( T ) ) = > E q − ( 2 ) \begin{aligned}
-div(q) = div(k \space grad(T))\\
=>Eq-(2)
\end{aligned} − d i v ( q ) = d i v ( k g r a d ( T ) ) = > E q − ( 2 )
Total Energy
The total energy is equal to the sum of work done (Eq. 1), Energy flux (Eq. 2) due to heat conduction, and stored potential energy due to gravity (S E S_{E} S E
So,
ρ D E D t = − d i v ( p U ) + ∂ ( u τ x x ) ∂ x + ∂ ( u τ y x ) ∂ y + ∂ ( u τ z x ) ∂ z + ∂ ( v τ x x ) ∂ x + ∂ ( v τ y x ) ∂ y + ∂ ( v τ z x ) ∂ z + ∂ ( w τ x x ) ∂ x + ∂ ( w τ y x ) ∂ y + ∂ ( w τ z x ) ∂ z + d i v ( k g r a d ( T ) ) + S E = > E q − ( 3 ) \begin{aligned}
\rho \frac{D E} {D t} &= -div(pU) + \frac{\partial (u\tau_{xx})}{\partial x} + \frac{\partial (u \tau_{yx})}{\partial y} + \frac{\partial (u \tau_{zx})}{\partial z} \\
&+ \frac{\partial (v \tau_{xx})}{\partial x} + \frac{\partial (v \tau_{yx})}{\partial y} + \frac{\partial (v \tau_{zx})}{\partial z} \\
&+ \frac{\partial (w\tau_{xx})}{\partial x} + \frac{\partial (w\tau_{yx})}{\partial y} + \frac{\partial (w \tau_{zx})}{\partial z}\\
&+ div(k \space grad(T)) + S_{E}\\
&=>Eq-(3)
\end{aligned}
ρ D t D E = − d i v ( p U ) + ∂ x ∂ ( u τ x x ) + ∂ y ∂ ( u τ y x ) + ∂ z ∂ ( u τ z x ) + ∂ x ∂ ( v τ x x ) + ∂ y ∂ ( v τ y x ) + ∂ z ∂ ( v τ z x ) + ∂ x ∂ ( w τ x x ) + ∂ y ∂ ( w τ y x ) + ∂ z ∂ ( w τ z x ) + d i v ( k g r a d ( T ) ) + S E = > E q − ( 3 )
Kinetic Energy
The kinetic energy can be calculated by multiplying the momentum equation by the velocity.
Below is the momentum equation from Momentum equation in a 3D particle and its surface & body forces
ρ D u D t = ∂ ( − p + τ x x ) ∂ x + ∂ ( τ y x ) ∂ y + ∂ ( τ z x ) ∂ z + S M x ρ D v D t = ∂ ( τ x x ) ∂ x + ∂ ( − p + τ y x ) ∂ y + ∂ ( τ z x ) ∂ z + S M y ρ D w D t = ∂ ( τ x x ) ∂ x + ∂ ( τ y x ) ∂ y + ∂ ( − p + τ z x ) ∂ z + S M z \begin{array}{c}
\rho \frac{Du}{Dt} = \frac{\partial (-p + \tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} + S_{Mx} \\\\
\rho \frac{Dv}{Dt} = \frac{\partial (\tau_{xx})}{\partial x} + \frac{\partial (-p + \tau_{yx})}{\partial y} + \frac{\partial (\tau_{zx})}{\partial z} + S_{My}\\\\
\rho \frac{Dw}{Dt} = \frac{\partial (\tau_{xx})}{\partial x} + \frac{\partial (\tau_{yx})}{\partial y} + \frac{\partial (-p+\tau_{zx})}{\partial z} + S_{Mz}\\\\
\end{array} ρ D t D u = ∂ x ∂ ( − p + τ x x ) + ∂ y ∂ ( τ y x ) + ∂ z ∂ ( τ z x ) + S M x ρ D t D v = ∂ x ∂ ( τ x x ) + ∂ y ∂ ( − p + τ y x ) + ∂ z ∂ ( τ z x ) + S M y ρ D t D w = ∂ x ∂ ( τ x x ) + ∂ y ∂ ( τ y x ) + ∂ z ∂ ( − p + τ z x ) + S M z
When we separate the pressure terms
ρ D u D t = − ∂ p ∂ x + ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z + S M x ρ D v D t = − ∂ p ∂ y + ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z + S M y ρ D w D t = − ∂ p ∂ z + ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z + S M z \begin{array}{c}
\rho \frac{Du}{Dt} = -\frac{\partial p}{\partial x} + \frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + S_{Mx} \\\\
\rho \frac{Dv}{Dt} = -\frac{\partial p}{\partial y} + \frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + S_{My}\\\\
\rho \frac{Dw}{Dt} = -\frac{\partial p}{\partial z} + \frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + S_{Mz}\\\\
\end{array} ρ D t D u = − ∂ x ∂ p + ∂ x ∂ τ x x + ∂ y ∂ τ y x + ∂ z ∂ τ z x + S M x ρ D t D v = − ∂ y ∂ p + ∂ x ∂ τ x x + ∂ y ∂ τ y x + ∂ z ∂ τ z x + S M y ρ D t D w = − ∂ z ∂ p + ∂ x ∂ τ x x + ∂ y ∂ τ y x + ∂ z ∂ τ z x + S M z
Since,
− ∂ p ∂ x − ∂ p ∂ y − ∂ p ∂ z = − g r a d p -\frac{\partial p}{\partial x} -\frac{\partial p}{\partial y} -\frac{\partial p}{\partial z} = -grad \space p − ∂ x ∂ p − ∂ y ∂ p − ∂ z ∂ p = − g r a d p
We can write the Kinematic equation as below,
ρ D 1 2 ( u 2 + v 2 + w 2 ) D t = − U . g r a d p + u ( ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z ) + v ( ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z ) + w ( ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z ) + U . S M = > E q − ( 4 ) \begin{array}{c}
\rho \frac{D \frac{1}{2}(u^2+v^2+w^2)} {D t} &= -U.grad \space p \\\\
&+ u(\frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z})\\\\
&+ v(\frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z})\\\\
&+ w(\frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z})\\\\
&+ U.S_{M}\\\\
&=>Eq-(4)
\end{array} ρ D t D 2 1 ( u 2 + v 2 + w 2 ) = − U . g r a d p + u ( ∂ x ∂ τ x x + ∂ y ∂ τ y x + ∂ z ∂ τ z x ) + v ( ∂ x ∂ τ x x + ∂ y ∂ τ y x + ∂ z ∂ τ z x ) + w ( ∂ x ∂ τ x x + ∂ y ∂ τ y x + ∂ z ∂ τ z x ) + U . S M = > E q − ( 4 )
Internal Energy
The internal energy can be calculated by subtracting the Kinetic energy (Eq. 4) from total energy (Eq. 3).
LHS
ρ D E D t = ρ D [ i + 1 2 ( u 2 + v 2 + w 2 ) ] D t \rho \frac{D E} {D t} = \rho \frac{D [i+\frac{1}{2}(u^2+v^2+w^2)]} {D t} ρ D t D E = ρ D t D [ i + 2 1 ( u 2 + v 2 + w 2 ) ]
ρ D [ i + 1 2 ( u 2 + v 2 + w 2 ) ] D t − ρ D [ 1 2 ( u 2 + v 2 + w 2 ) ] D t = ρ D [ i ] D t \rho \frac{D [i+\frac{1}{2}(u^2+v^2+w^2)]} {D t} - \rho \frac{D [\frac{1}{2}(u^2+v^2+w^2)]} {D t} = \rho \frac{D [i]} {D t} ρ D t D [ i + 2 1 ( u 2 + v 2 + w 2 ) ] − ρ D t D [ 2 1 ( u 2 + v 2 + w 2 ) ] = ρ D t D [ i ]
RHS
Since,
− d i v ( p U ) = − [ ( U . g r a d p ) + p d i v ( U ) ] -div(pU) = -[(U.grad \space p ) + p \space div(U)] − d i v ( p U ) = − [ ( U . g r a d p ) + p d i v ( U ) ]
Using the dot product rule (refer divergence rule )
∂ ( u τ x x ) ∂ x = u ∂ ( τ x x ) ∂ x + τ x x ∂ ( u ) ∂ x \frac{\partial (u\tau_{xx})}{\partial x} = u\frac{\partial (\tau_{xx})}{\partial x} + \tau_{xx} \frac{\partial (u)}{\partial x} ∂ x ∂ ( u τ x x ) = u ∂ x ∂ ( τ x x ) + τ x x ∂ x ∂ ( u )
And introducing a new source term S E − U . S M = S i S_{E} - U.S_{M} = S_{i} S E − U . S M = S i
ρ D [ i ] D t = − p d i v ( U ) + d i v ( k g r a d ( T ) ) + τ x x ∂ u ∂ x + τ y x ∂ u ∂ y + τ z x ∂ u ∂ z + τ x x ∂ v ∂ x + τ y x ∂ v ∂ y + τ z x ∂ v ∂ z + τ x x ∂ w ∂ x + τ y x ∂ w ∂ y + τ z x ∂ w ∂ z + S i = > E q − ( 5 ) \begin{aligned}
\rho \frac{D [i]} {D t} &= - p \space div(U) + div(k \space grad(T)) \\
&+ \tau_{xx}\frac{\partial u}{\partial x} + \tau_{yx} \frac{\partial u}{\partial y} + \tau_{zx} \frac{\partial u}{\partial z} \\
&+ \tau_{xx}\frac{\partial v}{\partial x} + \tau_{yx}\frac{\partial v}{\partial y} + \tau_{zx}\frac{\partial v}{\partial z} \\
&+ \tau_{xx} \frac{\partial w}{\partial x} + \tau_{yx} \frac{\partial w}{\partial y} + \tau_{zx} \frac{\partial w}{\partial z}\\
&+ S_{i}\\
&=>Eq-(5)
\end{aligned} ρ D t D [ i ] = − p d i v ( U ) + d i v ( k g r a d ( T ) ) + τ x x ∂ x ∂ u + τ y x ∂ y ∂ u + τ z x ∂ z ∂ u + τ x x ∂ x ∂ v + τ y x ∂ y ∂ v + τ z x ∂ z ∂ v + τ x x ∂ x ∂ w + τ y x ∂ y ∂ w + τ z x ∂ z ∂ w + S i = > E q − ( 5 )
Deriving Temperature Equation for Incompressible Fluid
For incompressible fluid
i = c T i = c \space T i = c T
Where, c - specific heat
d i v U = 0 div \space U = 0 d i v U = 0
We can rewrite Eq.5 from the above conditions, resulting in a temperature equation as below.
ρ c D T D t = d i v ( k g r a d ( T ) ) + τ x x ∂ u ∂ x + τ y x ∂ u ∂ y + τ z x ∂ u ∂ z + τ x x ∂ v ∂ x + τ y x ∂ v ∂ y + τ z x ∂ v ∂ z + τ x x ∂ w ∂ x + τ y x ∂ w ∂ y + τ z x ∂ w ∂ z + S i = > E q − ( 6 ) \begin{aligned}
\rho c \frac{D T} {D t} &= div(k \space grad(T)) \\
&+ \tau_{xx}\frac{\partial u}{\partial x} + \tau_{yx} \frac{\partial u}{\partial y} + \tau_{zx} \frac{\partial u}{\partial z} \\
&+ \tau_{xx}\frac{\partial v}{\partial x} + \tau_{yx}\frac{\partial v}{\partial y} + \tau_{zx}\frac{\partial v}{\partial z} \\
&+ \tau_{xx} \frac{\partial w}{\partial x} + \tau_{yx} \frac{\partial w}{\partial y} + \tau_{zx} \frac{\partial w}{\partial z}\\
&+ S_{i}\\
&=>Eq-(6)
\end{aligned} ρ c D t D T = d i v ( k g r a d ( T ) ) + τ x x ∂ x ∂ u + τ y x ∂ y ∂ u + τ z x ∂ z ∂ u + τ x x ∂ x ∂ v + τ y x ∂ y ∂ v + τ z x ∂ z ∂ v + τ x x ∂ x ∂ w + τ y x ∂ y ∂ w + τ z x ∂ z ∂ w + S i = > E q − ( 6 )
Deriving Enthalpy Equation for Compressible Fluids
The specific enthalpy(h)(total enthalpy per unit mass) of fluid is equal to the sum of internal energy (i) and the product of pressure § & specific volume (1 / ρ 1/\rho 1 / ρ
h = i + p ρ h = i + \frac{p}{\rho} h = i + ρ p
The total enthalpy (h 0 h_{0} h 0 1 2 ( u 2 + v 2 + w 2 ) \frac{1}{2}(u^2+v^2+w^2) 2 1 ( u 2 + v 2 + w 2 )
h 0 = h + 1 2 ( u 2 + v 2 + w 2 ) = i + p ρ + 1 2 ( u 2 + v 2 + w 2 ) = E + p ρ \begin{aligned}
h_{0} &= h + \frac{1}{2}(u^2+v^2+w^2)\\
&= i + \frac{p}{\rho} + \frac{1}{2}(u^2+v^2+w^2)\\
&= E + \frac{p}{\rho}
\end{aligned} h 0 = h + 2 1 ( u 2 + v 2 + w 2 ) = i + ρ p + 2 1 ( u 2 + v 2 + w 2 ) = E + ρ p
Now,
E = h 0 − p ρ = > E q − ( 7 ) \begin{aligned}
E = h_{0} - \frac{p}{\rho}\\
=>Eq-(7)
\end{aligned} E = h 0 − ρ p = > E q − ( 7 )
As described in Conservation of momentum and energy , we can write the Energy equation below.
ρ D E D t = ∂ ( ρ E ) ∂ t + d i v ( ρ E U ) \begin{aligned}
\rho \frac{DE}{Dt} = \frac{\partial (\rho E)}{\partial t} + div(\rho E U)
\end{aligned} ρ D t D E = ∂ t ∂ ( ρ E ) + d i v ( ρ E U )
Substituting Eq. 7 to the above we get,
ρ D ( h 0 − p ρ ) D t = ∂ ( ρ ( h 0 − p ρ ) ) ∂ t + d i v ( ρ ( h 0 − p ρ ) U ) = ∂ ( ρ h 0 ) ∂ t − ∂ p ∂ t + d i v ( ρ h 0 U ) − d i v ( p U ) \begin{aligned}
\rho \frac{D (h_{0} - \frac{p}{\rho})}{Dt} &= \frac{\partial (\rho (h_{0} - \frac{p}{\rho}))}{\partial t} + div(\rho (h_{0} - \frac{p}{\rho}) U)\\
&= \frac{\partial (\rho h_{0})}{\partial t} - \frac{\partial p}{\partial t} + div(\rho h_{0}U) - div(pU)
\end{aligned} ρ D t D ( h 0 − ρ p ) = ∂ t ∂ ( ρ ( h 0 − ρ p ) ) + d i v ( ρ ( h 0 − ρ p ) U ) = ∂ t ∂ ( ρ h 0 ) − ∂ t ∂ p + d i v ( ρ h 0 U ) − d i v ( p U )
Using Eq. 3 we can write the below equation
∂ ( ρ h 0 ) ∂ t − ∂ p ∂ t + d i v ( ρ h 0 U ) − d i v ( p U ) = − d i v ( p U ) + ∂ ( u τ x x ) ∂ x + ∂ ( u τ y x ) ∂ y + ∂ ( u τ z x ) ∂ z + ∂ ( v τ x x ) ∂ x + ∂ ( v τ y x ) ∂ y + ∂ ( v τ z x ) ∂ z + ∂ ( w τ x x ) ∂ x + ∂ ( w τ y x ) ∂ y + ∂ ( w τ z x ) ∂ z + d i v ( k g r a d ( T ) ) + S h \begin{aligned}
\frac{\partial (\rho h_{0})}{\partial t} - \frac{\partial p}{\partial t} + div(\rho h_{0}U) - div(pU)\\
= \\
-div(pU) + \frac{\partial (u\tau_{xx})}{\partial x} + \frac{\partial (u \tau_{yx})}{\partial y} + \frac{\partial (u \tau_{zx})}{\partial z} \\
+ \frac{\partial (v \tau_{xx})}{\partial x} + \frac{\partial (v \tau_{yx})}{\partial y} + \frac{\partial (v \tau_{zx})}{\partial z} \\
+ \frac{\partial (w\tau_{xx})}{\partial x} + \frac{\partial (w\tau_{yx})}{\partial y} + \frac{\partial (w \tau_{zx})}{\partial z}\\
+ div(k \space grad(T)) + S_{h}
\end{aligned}
∂ t ∂ ( ρ h 0 ) − ∂ t ∂ p + d i v ( ρ h 0 U ) − d i v ( p U ) = − d i v ( p U ) + ∂ x ∂ ( u τ x x ) + ∂ y ∂ ( u τ y x ) + ∂ z ∂ ( u τ z x ) + ∂ x ∂ ( v τ x x ) + ∂ y ∂ ( v τ y x ) + ∂ z ∂ ( v τ z x ) + ∂ x ∂ ( w τ x x ) + ∂ y ∂ ( w τ y x ) + ∂ z ∂ ( w τ z x ) + d i v ( k g r a d ( T ) ) + S h
∂ ( ρ h 0 ) ∂ t + d i v ( ρ h 0 U ) = ∂ p ∂ t + d i v ( k g r a d ( T ) ) + ∂ ( u τ x x ) ∂ x + ∂ ( u τ y x ) ∂ y + ∂ ( u τ z x ) ∂ z + ∂ ( v τ x x ) ∂ x + ∂ ( v τ y x ) ∂ y + ∂ ( v τ z x ) ∂ z + ∂ ( w τ x x ) ∂ x + ∂ ( w τ y x ) ∂ y + ∂ ( w τ z x ) ∂ z + S h \begin{aligned}
\frac{\partial (\rho h_{0})}{\partial t} + div(\rho h_{0}U) &= \frac{\partial p}{\partial t} +div(k \space grad(T))\\
&+\frac{\partial (u\tau_{xx})}{\partial x} + \frac{\partial (u \tau_{yx})}{\partial y} + \frac{\partial (u \tau_{zx})}{\partial z} \\
&+ \frac{\partial (v \tau_{xx})}{\partial x} + \frac{\partial (v \tau_{yx})}{\partial y} + \frac{\partial (v \tau_{zx})}{\partial z} \\
&+ \frac{\partial (w\tau_{xx})}{\partial x} + \frac{\partial (w\tau_{yx})}{\partial y} + \frac{\partial (w \tau_{zx})}{\partial z}\\
&+ S_{h}
\end{aligned}
∂ t ∂ ( ρ h 0 ) + d i v ( ρ h 0 U ) = ∂ t ∂ p + d i v ( k g r a d ( T ) ) + ∂ x ∂ ( u τ x x ) + ∂ y ∂ ( u τ y x ) + ∂ z ∂ ( u τ z x ) + ∂ x ∂ ( v τ x x ) + ∂ y ∂ ( v τ y x ) + ∂ z ∂ ( v τ z x ) + ∂ x ∂ ( w τ x x ) + ∂ y ∂ ( w τ y x ) + ∂ z ∂ ( w τ z x ) + S h